Il V postulato di Euclide: un dogma violato che cambiò il mondo.

Nel post precedente, abbiamo parlato dei primi 4 postulati di Euclide e di come possono essere usati per costruire l’intera geometria che abbiamo studiato a scuola.

Siamo rimasti in sospeso con la questione, delle rette parallele. Si incontrano o no ?

Il quinto postulato recita come segue:

5. Se una retta taglia altre due rette determinando dallo stesso lato angoli interni la cui somma è minore di quella di due angoli retti, prolungando le due rette, esse si incontreranno dalla parte dove la somma dei due angoli è minore di due retti.

Euclide è sempre stato molto dubbioso rispetto al quinto postulato, perché era convinto che fosse possibile derivarlo dagli altri quattro e, in definitiva, rimuoverlo dagli assiomi di base. Le sue perplessità derivavano da vari motivi. Il primo di questi è la complessità del postulato, decisamente maggiore dei primi quattro che sono molto più concisi.

Proviamo a comprendere il quinto postulato disegnandolo: tracciamo una retta r che intersechi le rette s e t in modo tale che gli angoli interni a e b abbiano somma inferiore a due angoli retti, cioè l’angolo piatto. Il quinto postulato dice che, sotto queste ipotesi, le rette s e t si incontrano in un punto che giace dal lato dei due angoli a e b. Un altro modo per esprimere lo stesso postulato è dire che due rette parallele non si incontrano mai.

Questo postulato non deve essere mai piaciuto molto ad Euclide, infatti negli Elementi usò esclusivamente i primi quattro per costruire le 28 proposizioni alla base del corpus di teoremi che Euclide stesso definì Geometria Assoluta. Tra queste c’è la proposizione fondamentale che asserisce che per un punto passano infinite rette.

Il quinto postulato è usato negli Elementi in casi particolari e, comunque, Euclide lo consegnò all’umanità col dubbio che fosse derivabile dagli altri quattro. La questione dell’indipendenza del quinto postulato dagli altri quattro tenne impegnate le più grandi menti matematiche per oltre 2000 anni.

Basti menzionare la storia di Padre Giovanni Girolamo Saccheri che pubblicò nel 1733 – poco prima di morire – una dimostrazione in cui si tentò di dimostrare per assurdo il quinto postulato supponendolo falso per poi ottenere una contraddizione. Padre Saccheri credette di aver trovato la contraddizione cercata, ma si sbagliò. Quindi non si rese conto che la sua dimostrazione non era formalmente corretta ma, nel commettere questo errore, gettò le basi per le geometrie non euclidee. Padre Saccheri morì convinto di aver sprecato anni, ma se solo avesse saputo …

In pratica, dall’opera di Padre Saccheri si deduce che è possibile sia ammettere che non ammettere vero il quinto postulato di Euclide ed ottenere, in questo modo, geometrie perfettamente equivalenti, fatto salvo un opportuno processo di trasformazione. Ciò vuol dire che le due ipotesi:

• Due rette parallele non si incontrano all’infinto.
• Due rette parallele si incontrano all’infinto.

Sono entrambe ugualmente ammissibili. Al di là del meccanismo di dimostrazione adottato da Padre Saccheri, ricordate un fatto chiave che abbiamo esposto sopra ? Il quinto postulato è una ipotesi che abbiamo adottato come vera, ma non è necessariamente vera. Ora facciamo un esercizio inverso: supponiamo che non sia vero e cerchiamo di pensare ad un concetto di parallelismo compatibile con questa scelta.

Un indizio: guardate i vostri piedi e l’orizzonte, l’oggetto che risolve questo problema è proprio qui davanti e intorno a voi, è enorme. Il pianeta terra !

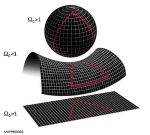
Il genere umano è stato ingannato per lunghissimo tempo dal fatto che la terra è talmente grande da sembrare piatta, ma così non è. Prolungando all’infinito due rette parallele disegnate sulla superficie terrestre, queste si incontrano e come: ai due poli. Questa strana geometria ha diverse peculiarità: un triangolo disegnato sulla superficie terrestre ha somma degli angoli interni minore di 180°, ad esempio. Ciò accade perché nella geometria ellittica i segmenti giacciono in “rette” che sono in realtà oggetti curvi (geodetiche).

Il lavoro di Euclide è impressionante: tutta la geometria assoluta, ovvero quella costruita sulle 28 proposizioni fondamentali, a loro volta derivate dai primi quattro postulati vale anche per le geometrie non euclidee, compresa quella ellittica.

Padre Saccheri aprì le porte ad un impianto concettuale potentissimo: le geometrie non euclidee. Pensate, fu solamente nel 1828 che Gauss segnò una svolta nell’indagine delle geometrie non euclidee le quali verranno infine formalizzate da Riemann, Beltrami, Poincaré e Hilbert solamente all’inizio del 1900.

La meravigliosa storia di Euclide e dei tanti matematici che si avvicendarono nei 2200 anni successivi insegna, ancora una volta, che la scienza è fatta da uomini di ingegno ed intelletto fine, che cambia e non è mai dogmatica. Ed è grazie a questa capacità di mettere in discussione le idee, riformulandone di nuove e più potenti, che oggi possiamo usare le meraviglie della tecnologia moderna.

Ma allora, due rette parallele si incontrano ? Si, se lo vogliamo …

PODCAST004