 Chiudiamo il ciclo sul paradosso del compleanno per raccontare il concetto di eleganza in matematica. Vi sembra strano, lo so, eppure per il matematico l’eleganza è importante quanto (e forse più) per lo stilista.
Chiudiamo il ciclo sul paradosso del compleanno per raccontare il concetto di eleganza in matematica. Vi sembra strano, lo so, eppure per il matematico l’eleganza è importante quanto (e forse più) per lo stilista.
Il concetto di eleganza è però legato a fattori più sottili e dalle diverse sfaccettature. In questo post ne vediamo una: la compattezza. Tanto più compatta, cioé breve, è una formulazione matematica, tanto più è ricercata. Un po’ come per la magrezza delle modelle, in matematca la compattezza è fondamentale perché consente di applicare le formule matematiche adottando un numero di termini che sia il minore possibile.
Il paradosso del compleanno si applica bene all’illustrazione del concetto di compattezza, perché la probabilità che N persone NON siano nate lo stesso giorno è data dal prodotto di N – 1 termini, lo abbiamo visto la volta scorsa, quindi da una espressione di lunghezza variabile.
Con due persone abbiamo un solo termine:
P(2) = 364/365
con tre persone i termini diventano due:
P(3) = 364/365 x 363/365
con N persone i termini sono N – 1
P(N) = 364/365 x 363/365 x 362/365 x …
Siamo rimasti al post precedente con un mero elenco di questi termini, ma se volessimo usarne l’espressione per sostituirla in un altro calcolo, non potremmo farlo perché è costituita da un numero di termini variabile. Ci serve una formula.
Vediamo un po’ se nella nostra borsa del matematico c’è un ferro adatto per questo problema … uhmmm … eccone uno: la produttoria. Ricordate ? Con il simbolo di produttoria possiamo esprimere il prodotto di un numero arbitrario di termini, proprio quello che serve a noi.
La produttoria ha un indice, in questo caso usiamo la p per indicare il termine corrispondente al numero di persone corrente, ed N per indicare il numero di persone complessivo. Usiamola per moltiplicare N – 1 termini, adottando la variabile p per contare da 1 al numero massimo di persone meno una, cioé N – 1.
Analizzando i singoli termini vediamo che sono composti da frazioni: al denominatore c’è sempre 365 e al numeratore figura un numero decrescente, sempre pari a 365-p+1. Con due persone (p = 2) abbiamo infatti che la frazione è 365 – 2 + 1 = 364, con tre (p = 3) è 365 – 3 + 1 = 363, e così via. L’espressione della probabilità che N persone non siano nate lo stesso giorno è quindi:
Abbiamo ottenuto una espressione che può essere sostituita in altri calcoli perché compatta, non una lista indefinita di termini, ingestibile. Questa espressione è più elegante perchè usabile e, soprattutto, è più breve: compatta, appunto. Possiamo ritenerci soddisfatti ?
L’intuizione del matematico, vedendo una espressione del genere, va immediatamente in fibrillazione. Guardate il denominatore: il prodotto di 365 per se stesso N – 1 volte è ovviamente una potenza: 365^(N-1). Resta il numeratore, un pò più ostico da rendere compatto. Se riuscissimo a scrivere una espressione unica per tutta la serie di prodotti al numeratore, potremmo rendere ancora più compatta, quindi elegante, l’espressione complessiva.
Frughiamo ancora nella borsa del matematico, vediamo se c’è qualche altro strumento che ci torna utile … dunque … ci serve un prodotto di termini. Ah ecco: il fattoriale. Osservate ancora l’espressione della probabilità per tre persone:
P(3) = 364/365 x 363/365
al denominatore figura 365^2. mentre al numeratore c’è il prodotto di 364 per 353. Possiamo esprimerlo mediante il fattoriale ? Certo, basta rimuovere da 364! (364 fattoriale) tutti i termini da 362 in giù, cioé dividere per 362!, e l’espressione di P(3) diviene:
guarda caso, 362 è pari a 365 meno il numero di persone per cui stiamo calcolando la probabilità, cioé 3. Da qui, la generalizzazione per un numero arbitrario N di persone è davvero ad un passo. Al numeratore c’è sempre 364! e al denominatore abbiamo N-1 volte il prodotto di 365 e (365 – N) ! per semplificare i termini in eccesso al numeratore:
La probabilità che N persone siano nate lo stesso giorno è quindi 1 – P(N). Osservate attentamente l’uso che abbiamo fatto delle potenze e del fattoriale per calcolare la probablità. In realtà, abbiamo usato questi due strumenti per determinare le combinazioni possibili per il problema specifico. Potenze e fattoriale giocano un ruolo fondamentale nella matematica combinatoria. Ci torneremo su.
Intanto, contemplate la formula: non è elegante ?



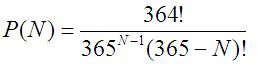

Sono pienamente d’accordo.
L’eleganza nella matematica e’ importante…ed io amavo scrivere le formula..soprattutto gli integrali.
Pingback: L'eleganza non è mai banale