In tempi di riforma elettorale ci dedichiamo ad un esercizio di pura fantasia che, tuttavia, può tornare utile. Inciucio di Sotto è una ridente località di villeggiatura con forti interessi commerciali e grande attrattiva turistica e deve affrontare una importante prova elettorale. Il Commendator De Furbastris del comune di Inciucio di Sotto ha una grande influenza sui suoi elettori, per così dire.
Il Commendator De Furbastris controlla 1008 elettori e ha interesse a far eleggere 10 candidati. Le schede prevedono 5 preferenze. Quanti voti riesce ad assegnare a ciascun candidato?
De Furbastris, che mastica di matematica, decide di assegnare una combinazione di preferenze specifica a ciascuno degli elettori che controlla , in modo da equidistribuire i voti tra i propri candidati. Il numero di combinazioni di n oggetti, presi a gruppi di k è dato dal Binomio di Newton:
Ove n! si legge “n fattoriale” ed è il prodotto dei primi n numeri interi (vedi approfondimento a fine articolo). In italiano si legge “n su k” e, sostituendo i valori del caso specifico – 10 candidati e 5 preferenze – abbiamo
= 252 combinazioni
Identificando i candidati con le lettere a,…,f, vediamo alcune combinazioni di esempio:
{a,b,c,d,e} {a,b,c,d,f} {a,b,c,d,g} {a,b,c,d,h} {a,b,c,d,i} {a,b,c,d,j} …
De Furbastris, che abbiamo detto controlla i votanti, decide di assegnare la prima combinazione al primo votante, la seconda al secondo e così via fino alla 252ma al 252mo votante, per poi riniziare da capo con la prima combinazione al 253mo e così via. Su 1008 elettori il Commendatore riuscirà ad assegnare esattamente
1008/252 = 4
volte il giro di tutte le combinazioni possibili.
Per ciascun giro di preferenze, ogni candidato riceverà un certo numero di voti. Per sapere quanti voti in totale riuscirà ad assegnare a ciascun candidato dovremo calcolare quanti voti si ricevono complessivamente per ciascuna tornata di 252 combinazioni.
Questo numero si determina nuovamente attraverso il Binomio di Newton, osservando che il candidato “a” appare nelle combinazioni sempre occupando una preferenza, ovvero riducendo contemporaneamente sia il numero di candidati, sia il numero di preferenze disponibili. Nel caso specifico in un numero di combinazioni pari a 9 su 4,
= 126 combinazioni.
Il numero di voti che ciascun candidato prenderà sarà quindi pari a
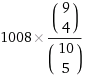
= 504 voti
La cosa più interessante è che, nel caso generico di C votanti controllati, n candidati e k preferenze, abbiamo che il rapporto tra i due Binomi di Newton:
si semplifica e vale esattamente il rapporto k/n (torneremo sulla dimostrazione in un post successivo). Questo significa che l’applicazione di un sistema a preferenze equivale a tutti gli effetti a campionare la base di votanti, e che valgono tutti i teoremi del campionamento.
Nel caso concreto, il rapporto k/n vale 0.5 e il numero di voti risultante è pari a 1008/2=504. Un sistema di votazione a 5 preferenze con 10 candidati equivale a campionare al 50% la base di elettori controllati. All’atto pratico, attraverso le preferenze, è possibile non solo controllare il comportamento dei votanti ma anche di stabilire chi di questi è “infedele” e non ha rispettato i patti, per così dire, attraverso opportune statistiche sulla distribuzione dei voti ottenuta alle urne.
Ci torneremo su.
-> Vai all’approfondimento sul fattoriale
